Andragradsekvation
Använd vår räknare nedan för att snabbt lösa en andragradsekvation, eller scrolla ner för att lära dig hur man löser en andragradsekvation steg för steg.
Räknare: Andragradslösare
Kalkylatorn räknar ut rötterna \(x_1\) och \(x_2\) till andragradsekvationen \(Ax^2 + Bx + C = 0\).
Hur använder man vår andragradslösare?
För att använda vår andragradslösare måste du först identifiera koefficienterna \(A\), \(B\) och \(C\) i din andragradsekvation. Här nedan hittar du ett par exempel som visar hur du kan identifiera dessa koefficienter och använda dem i vår kalkylator.
Exempel 1:
\( \mathbf{2x^2 - 3x + 5 = 0}\)
\(\Leftrightarrow 2x^2 + (-3)x + 5 = 0 \)
\(\Rightarrow A = 2, \, B = -3, \, C = 5\)
\(B\)-värdet är negativt eftersom koefficienten till \( x \) är negativ.
Exempel 2:
\( \mathbf{2x^2 - 4x + 1 = -6x - 5} \)
\(\Leftrightarrow 2x^2 + 2x + 6 = 0\)
\(\Rightarrow A = 2, \, B = 2, \, C = 6\)
I exemplet ovan har termerna flyttats till vänster led för att få ekvationen att vara lika med noll.
Exempel 3:
\( \mathbf{x^2 - 9 = 0} \)
\(\Leftrightarrow 1x^2 + 0x - 9 = 0\)
\(\Rightarrow A = 1, \, B = 0, \, C = -9\)
I det här exemplet är \(B\)-koefficienten noll eftersom det saknas en x-term.
PQ formeln
PQ-formeln är en metod som används för att lösa andragradsekvationer av formen \( x^2 + px + q = 0 \). Här är formeln:
\[ x = -\frac{p}{2} \pm \sqrt{\left( \frac{p}{2} \right)^2 - q} \]
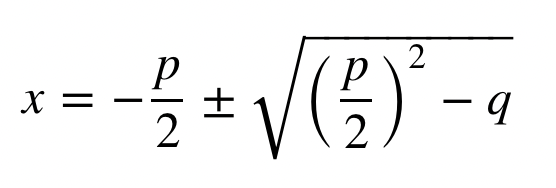
Där \( p \) och \( q \) är koefficienterna från ekvationen \( x^2 + px + q = 0 \).
Så här används PQ-formeln:
- Identifiera koefficienterna \( p \) och \( q \) i ekvationen \( x^2 + px + q = 0 \).
- Sätt in dessa värden i PQ-formeln: \( x = -\frac{p}{2} \pm \sqrt{\left( \frac{p}{2} \right)^2 - q} \)
- Räkna ut \( x_1 \) och \( x_2 \).
Andragradsekvation exempel
\( x^2 - 4x + 3 = 0 \)
Steg 1: Identifiera \( p \) och \( q \)
- \(p = -4\)
- \(q = 3\)
Steg 2: Använd PQ-formeln
\(x = -\frac{-4}{2} \pm \sqrt{\left( \frac{-4}{2} \right)^2 - 3} \)
\( \Leftrightarrow x = 2 \pm 1\)
Steg 3: Räkna ut \( x_1 \) och \( x_2 \)
- \( x_1 = 2+1=3\)
- \( x_2 = 2-1=1\)
Svar: Rötterna till ekvationen \( x^2 - 4x + 3 = 0 \) är \( x_1 = 3 \) och \( x_2 = 1 \).