Parallellogram area och omkrets
Använd vår räknare nedan för att smidigt och enkelt beräkna arean av en parallellogram.
Räknare: Parallellogram
Parallellogrammens area
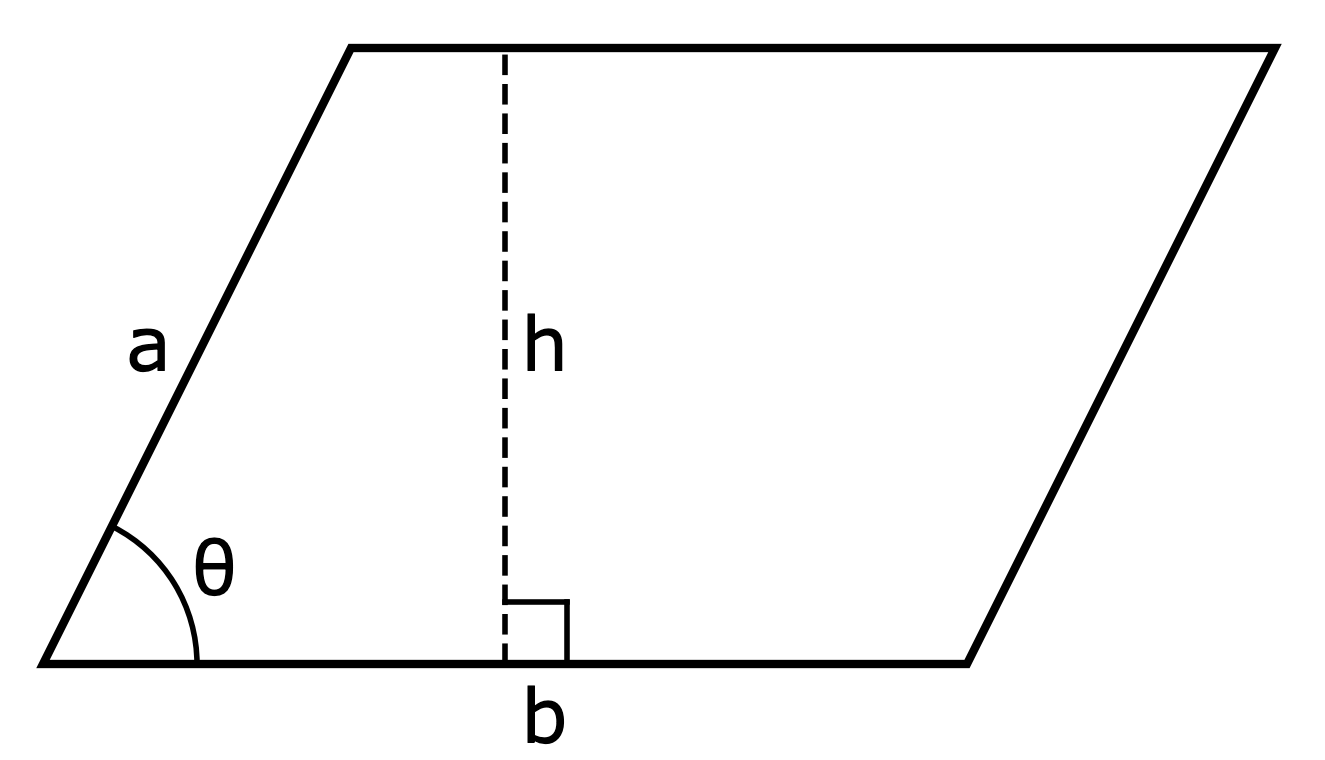
För att beräkna arean $A$ av en parallellogram används en formel som liknar den för rektanglar. Istället för längden och bredden använder man basen $b$ och höjden $h$, där höjden är det vinkelräta avståndet från basen till den motsatta sidan. Formeln för arean ges av:
$$A = b \cdot h$$
Man kan även beräkna arean av en parallellogram utan att känna till höjden. Om man känner till längderna på två sidor i en parallellogram, $a$ och $b$, samt vinkeln $\theta$ mellan dem, så kan man räkna ut arean med följande formel:
$$A = a \cdot b \cdot \sin(\theta)$$
Parallellogrammens omkrets
Du beräknar omkretsen av en parallellogram genom att summera längden av alla dess sidor. Eftersom en parallellogram har två par av parallella sidor som är lika långa, beräknas omkretsen som:
$$O = 2a + 2b$$
Vinkelsumma parallellogram
Vinkelsumman i en parallellogram är alltid 360 grader. Detta gäller för alla typer av parallellogrammer, inklusive rektanglar och kvadrater.